Our approach was the following:
- Wrote a python script to connect to the CSAW server and complete a SHA-1 proof-of-work
- Determined the follow-on cipher to be FEAL-4
- Researched attacks on FEAL-4 and found it vulnerable to differential cryptanalysis
- Found slight differences between CSAW's FEAL-4 implementation and the standard version
- Adjusted differential cryptanalysis attack to fit CSAW's modified implementation of FEAL-4
SHA-1 Proof-of-Work
Upon connecting to the server, we see the following:
The server sends 12 random bytes encoded into base64. The goal is to send back a SHA-1 hash which begins with those 12 bytes and ends with all 1 bits.
The server sends 12 random bytes encoded into base64. The goal is to send back a SHA-1 hash which begins with those 12 bytes and ends with all 1 bits.
Our client code receives those 12 prefix bytes and generates a SHA-1 hash till it matches:
FEAL Cipher
After completing the proof-of-work, the server greets you with the message:
The number after "Please decrypt: " is the flag encrypted with a random key which changes on each connection.
As far as we could tell, there is no feal 4.3 cipher, there is only FEAL-4, FEAL-8, and FEAL-N, where the numbers 4, 8, and N indicate the number of rounds of the cipher. Here is an excerpt from the wikipedia page on FEAL:
The number after "Please decrypt: " is the flag encrypted with a random key which changes on each connection.
As far as we could tell, there is no feal 4.3 cipher, there is only FEAL-4, FEAL-8, and FEAL-N, where the numbers 4, 8, and N indicate the number of rounds of the cipher. Here is an excerpt from the wikipedia page on FEAL:
In cryptography, FEAL (the Fast data Encipherment ALgorithm) is a block cipher proposed as an alternative to the Data Encryption Standard (DES), and designed to be much faster in software. The Feistel based algorithm was first published in 1987 by Akihiro Shimizu and Shoji Miyaguchi from NTT. The cipher is susceptible to various forms of cryptanalysis, and has acted as a catalyst in the discovery of differential and linear cryptanalysis.
An impressive page on cryptography and cryptanalysis is TheAmazingKing.com by Jon King. He even has a page on differential cryptanalysis of the FEAL-4 cipher. It includes a video, a tutorial with diagrams, and source code. Below are diagrams of the FEAL-4 cipher with permission from King. Please visit his page if you'd like a more in-depth explanation the cipher and its cryptanalysis.
Here we see the cipher has four rounds and six subkeys.
Each round has a round function, also known as an F-Box, and each F-box contains four G-Boxes.
Here we see the cipher has four rounds and six subkeys.
 |
| http://www.theamazingking.com/crypto-feal.php |
 |
| http://www.theamazingking.com/crypto-feal.php |
Differential Cryptanalysis
At a high level, differential cryptanalysis is a chosen plaintext attack that works by generating plaintext messages with a known relationship and tracing how that relationship changes at each round of the encryption. Determining how the relationship changes leaks information about the subkeys.
The first step is generating a random plaintext. The next is to derive a second plaintext by XORing the first with a specific number called the differential. The differential is chosen based on how the encryption rounds of a particular cipher affect it. In the case of FEAL-4, we generate three sets of plaintext pairs, each set of pairs has a differential that is specific to a round. There are three sets of plaintext pairs and differentials instead of four because the first round requires an approach closer to brute-force. In addition to the three input differentials that correspond to three rounds, there is an expected output differential. Combining these known input and output relationships allows us to dramatically shrink the space of the subkeys and brute-force them.
Running this differential cryptanalysis attack against CSAW's version of FEAL-4 did not work though. In the following section, I highlight why and what we did to fix it.
Running this differential cryptanalysis attack against CSAW's version of FEAL-4 did not work though. In the following section, I highlight why and what we did to fix it.
CSAW's Version of FEAL: feal 4.3
There was one slight difference in feal 4.3 versus the standard FEAL-4 cipher. That difference was the cyclical bit shift inside the G-Boxes. See the diagrams from the FEAL-4 section above. feal 4.3 had a cyclic bit shift of 3 and the standard FEAL-4 has only a cyclic bit shift of 2.
feal 4.3 python code:
Standard FEAL-4 code from King:
The greeting "Welcome to feal 4.3" given after the SHA-1 proof-of-work seems to hint towards this change. This modified bit shift in the encryption algorithm required us to change our cryptanalysis to account for it. We changed the third input differential from 0x0000000002000000 to 0x0000000004000000, just an extra bit shift. We verified this adaptation by modifying King's implementation to do a bit shift of 3 in the encryption and confirmed King's cracker could only extract subkeys with our new differential.
Endianness
There was possibly a second difference in feal 4.3. It may have been due to something we did or maybe it was the way CSAW implemented its algorithm, or both.
We think the way the F-boxes were implemented in CSAW's feal 4.3 differed from that provided by King. We could not get ciphertexts from CSAW's version to match King's. This was until we swapped the bytes in the F-box in King's C code, as in swap(x0, x3) and swap( x1, x2). This led us to matching ciphertexts between the CSAW's version and King's version. To isolate this detail, we stepped through and verified every bit shift between the two versions.
Assuming King's implementation is correct, which we believe it is, there may have been some endianness issues in the python code. Another possibility is that issues could have come from the way we were sending the plaintext to the server. We experimented with sending little endian and big endian plaintexts.
After verifying that King's code and CSAW's were encrypting identically, we noticed the differential cryptanalysis attack stopped working. This is because swapping the bytes in our F-box required us to again change the differentials. We changed the third input differential again and now also the output differential from 0x0000000004000000 to 0x0000000000000004. With these changes we were able to successfully mount a differential cryptanalysis attack to extract all six subkeys from the ciphertext generated by CSAW's server.
Assuming King's implementation is correct, which we believe it is, there may have been some endianness issues in the python code. Another possibility is that issues could have come from the way we were sending the plaintext to the server. We experimented with sending little endian and big endian plaintexts.
After verifying that King's code and CSAW's were encrypting identically, we noticed the differential cryptanalysis attack stopped working. This is because swapping the bytes in our F-box required us to again change the differentials. We changed the third input differential again and now also the output differential from 0x0000000004000000 to 0x0000000000000004. With these changes we were able to successfully mount a differential cryptanalysis attack to extract all six subkeys from the ciphertext generated by CSAW's server.
Endgame
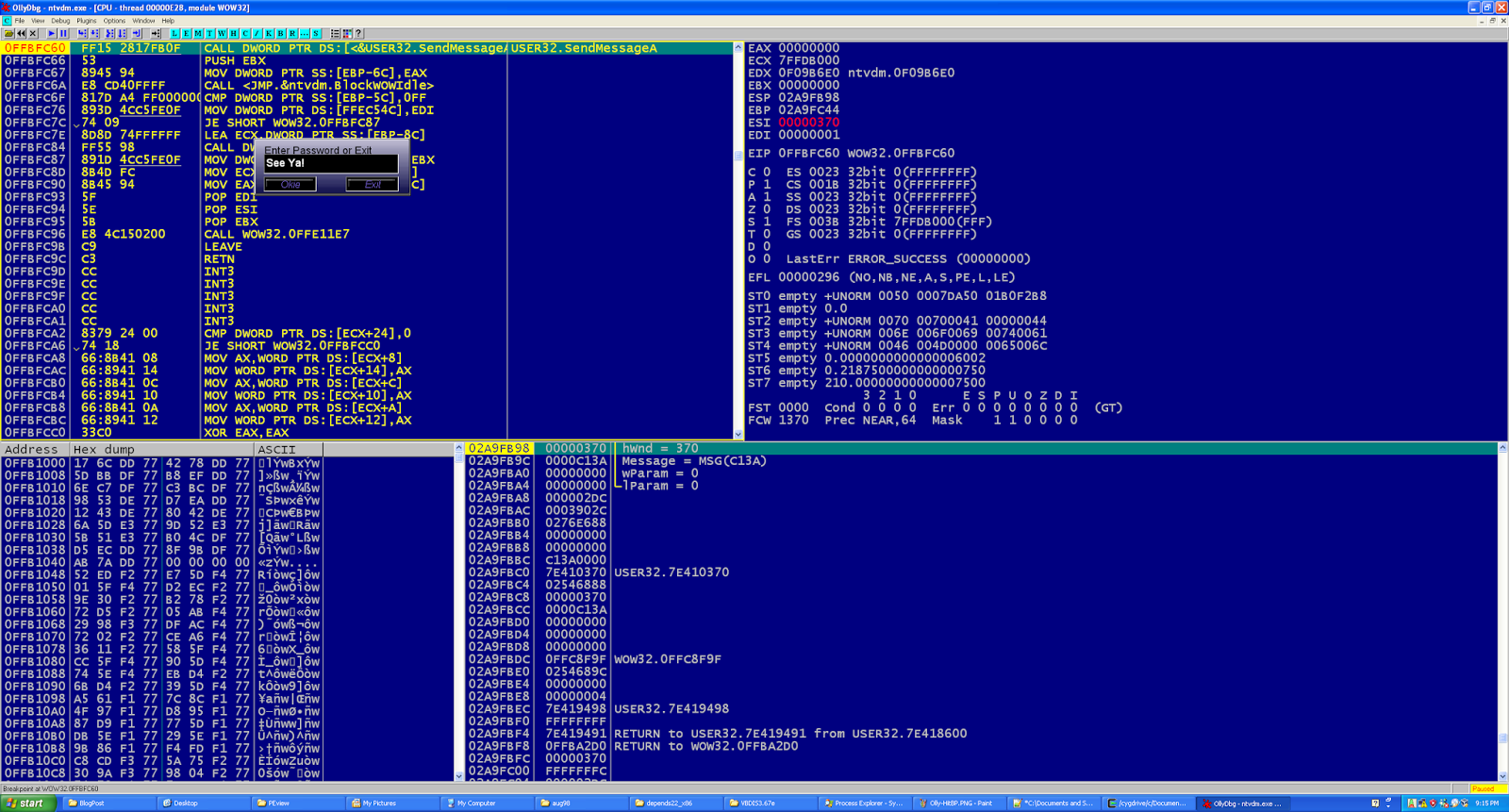
With only 5 minutes left in the CTF, we got the 6 subkeys. Our screenshot says Bad subkeys because of some debug code we left in it. Seeing the screen below was a powerful moment after 24 hours of work.
Then it got a bit chaotic. I read the hex bytes out loud to Unix-dude, who also sent them to Sliden. They both tried to decrypt the flag and submit it to the server.
It was a dramatic finish and the most fun I've ever had in a CTF. Thank you CSAW organizers and thank you Jon King. I look forward to learning more about cryptography.